Lecture 09 - Newton Spacetime is Curved

#math

Newton's Laws of motion

Newton I: A body on which no force acts moves uniformly along a straight line.
Newton II: Deviation (a.k.a acceleration) of a body's motion from such uniform straight motion is affected by a force, reduced by a factor of the body's reciprocal mass.

Notice that if one reads the first postulate as how a particle acts under force then its just a special case of the second postulate. Thus in order for the first postulate to be of use one could use it experimentally to figure out what a 'straight line' is in space, i.e testing the geometry of space.

Since gravity universally acts on every particle, in a universe with atleast two particles gravity must not be considered a force if 'Newton I' is supposed to remain applicable!

Laplace's Question: Can gravity be encoded in a curvature of space such that its effects show if a particles under the influence of (no other) force are postulated to move along straight lines in this curves space?
Answer: No!

Proof

Gravity is a force point of view:

m {\ddot{x}}^{α} (t) = m f^{α} (x (t))

Naturally we can cancel out the $m$ both sides which is what we see experimentally. Giving us:

{\ddot{x}}^{α} (t) = f^{α} (x (t))

One can rewrite the equation to be:

{\ddot{x}}^{α} (t) - f^{α} (x (t)) = 0

Laplace asks whether the above equation be rewritten to be:

{\ddot{x}}^{α} (t) + Γ^{α}_{β γ} (x (t)) {\dot{x}}^{β} {\dot{x}}^{γ} = 0

i.e as an autoparallel curve equation?
Well no since $Γ^{α}_{β γ} (x (t)) {\dot{x}}^{β} {\dot{x}}^{γ}$ depends on $\dot{x}$ while $f^{α}$ doesn't. We cannot find $Γ$ s such that Newton's equation takes the form of an autoparallel curve.

The full wisdom of Newton I

Use also the info from Newton's first law that particles (under no force) move uniformly.

The insight is in space-time uniform and straight motion in space is simply a straight motion!
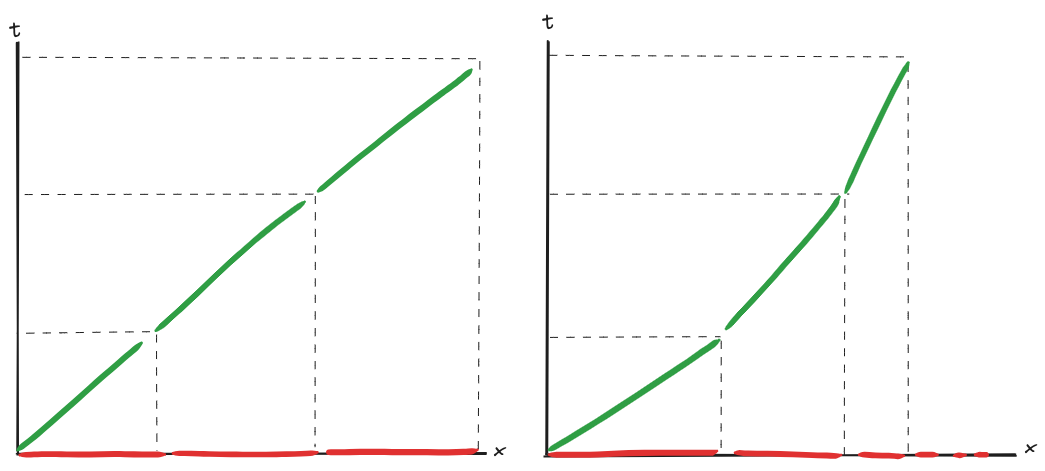
Pasted image 20231204193312.png|normal
So lets try in spacetime:

Let $x : R \to R^{3}$ be a particle's trajectory in space $\leftrightarrow$ worldline (history) of the particle

\begin{aligned} X : & R \to R^{4} \\ t \to (t, x^{1} (t), x^{2} (t), x^{3} (t)) = (X^{0} (t), X^{1} (t), X^{2} (t), X^{3} (t)) \end{aligned}

Pasted image 20231204194109.png
Trivial rewritings:
${\dot{X}}^{0} = 1$
This gives us:

\begin{aligned} {\ddot{X}}^{0} & = 0 \\ {\ddot{X}}^{α} - f^{α} \cdot {\dot{X}}^{0} \cdot {\dot{X}}^{0} & = 0. \end{aligned}

Which is equivalent to the autoparallel equation with $Γ^{0}_{a b} = Γ^{α}_{β γ} = Γ^{α}_{β 0} = Γ^{α}_{0 γ} = 0$ and only $Γ^{α}_{00} = - f^{α}$ .

This is also not a coordinate choice artifact since we can calculate $R^{α}_{0 β 0} = \frac{- \partial}{\partial_{β}} f^{α}$ (only non vanishing component) and $R_{00} = - \partial_{α} f^{α} = 4 π G ρ$ by Poisson's Law $(- \partial_{α} f^{α} = 4 π G ρ)$ .

Thus Laplace's idea works on spacetime!

The foundations of the geometric formulation of Newton's axioms

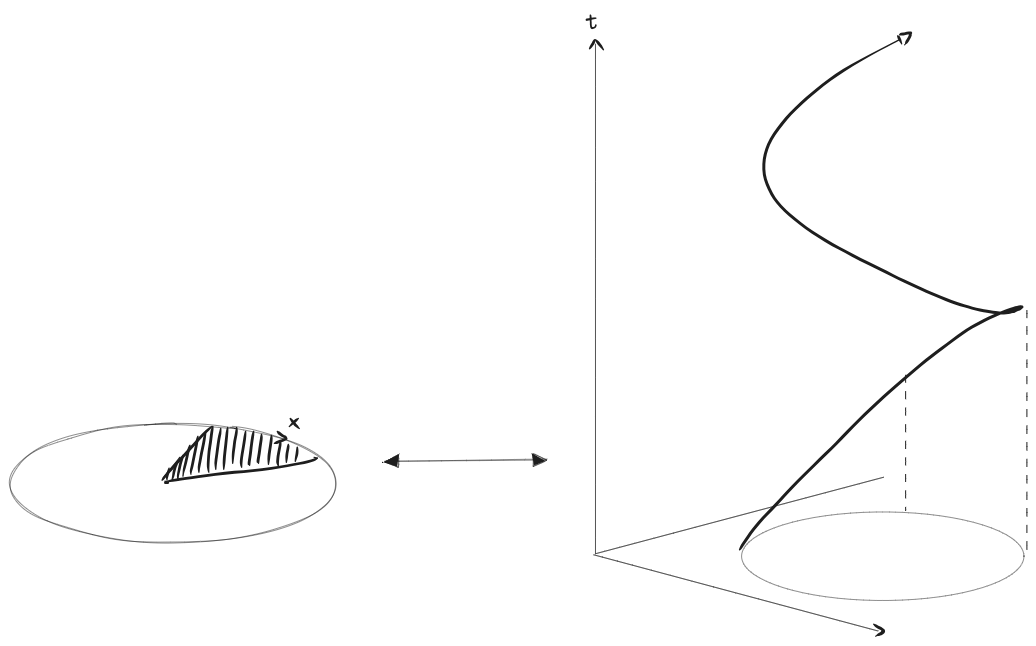
A Newtonian spacetime is a quintuple of structures $(M, O, A, \nabla, t)$ where $(M, O, A)$ $4$ -dim. smooth manifold and $t : M \to R$ is a smooth function, and Newton says:
a) "There is absolute space"

d t \neq 0 \forall p \in M

Absolute space at time $τ$ :

S_{τ} := {p \in M | t (p) = τ}

$⟹ M = ⋃ S_{τ}$ (i.e spacetime could be seen as a disjoint union of spaces, this is why we require the derivative to be non vanishing.)
b) "Absolute time flows uniformly" $⟹$ $\nabla d t = 0$ everywhere.
c) $\nabla$ is torsion free.

Definition

A vector $X \in T_{p} M$ is called:
a) future-directed if

d t (X) > 0

b) spatial if

d t (X) = 0

c) past-directed if

d t (X) < 0

Newton I: The worldlines of a particle with the influence of no force is a future directed autoparallel.
Newton II: $\nabla_{v_{X}} v_{X} = \frac{F}{m}$ where $F$ is a spatial vector field: $d t (F) = 0$ .

Convention: Restrict attention to atlases $A_{stratified}$ whose charts $(U, x)$ have the property that $x^{0} = t |_{U}$ (absolute time function). In a stratified atlas $0 = \nabla d t = \nabla_{\frac{\partial}{(\partial x^{a})}} d x^{0} = - Γ^{0}_{b a} .$

Lets evaluate in a chart $(U, x)$ of a stratified atlas $A_{strat}$ . Newton II says:

\nabla_{v_{X}} v_{X} = \frac{F}{m} .

In an arbitrary chart it takes the following form:

\begin{aligned} X^{0}^{″} + Γ^{0}_{c d} X^{c}^{'} X^{d} & = 0 \\ X^{α}^{″} + Γ^{α}_{γ δ} X^{γ}^{'} X^{δ}^{'} + Γ^{α}_{00} X^{0}^{'} X^{0}^{'} + 2 Γ^{α}_{γ 0} X^{γ}^{'} X^{0}^{'} & = \frac{F^{α}}{m} \end{aligned}

But in a stratified atlas the first equation simplifies down to:

\begin{aligned} {\ddot{X}}^{0} & = 0 \end{aligned}

Giving us: $X^{0} (λ) = a λ + b$ .
Convention: Parameterize world line by absolute time. i.e

a^{2} ({\ddot{X}}^{α} + Γ^{α}_{γ δ} {\dot{X}}^{γ} {\dot{X}}^{δ} + Γ^{α}_{00} {\dot{X}}^{0} {\dot{X}}^{0} + 2 Γ^{α}_{γ 0} {\dot{X}}^{γ} {\dot{X}}^{0}) = \frac{F^{α}}{m}

Giving us:

{\ddot{X}}^{α} + Γ^{α}_{γ δ} {\dot{X}}^{γ} {\dot{X}}^{δ} + Γ^{α}_{00} {\dot{X}}^{0} {\dot{X}}^{0} + 2 Γ^{α}_{γ 0} {\dot{X}}^{γ} {\dot{X}}^{0} = \frac{1}{a^{2}} \frac{F^{α}}{m}

${\ddot{X}}^{α} + Γ^{α}_{γ δ} {\dot{X}}^{γ} {\dot{X}}^{δ} + Γ^{α}_{00} {\dot{X}}^{0} {\dot{X}}^{0} + 2 Γ^{α}_{γ 0} {\dot{X}}^{γ} {\dot{X}}^{0}$ (Left hand side) is the acceleration vector!