Lecture 09 - Surface

#math

Idea

Let $M$ be a 2-dimensional surface embedded in a 3-dimensional space (or in general you can also embed it in any higher dimensional space). We want to assign a coordinate system on this surface and to do this we cover the surface in patches (which we will denote by $U_{α}$ ) who we can 'locally' map out flatly on $R^{2}$ (with a function $σ : U \subset R^{2} \to M$ ) one can imagine the surface of the earth where we have flat maps only for local regions. These local maps are called 'charts'.

The above idea encapsulates the idea of a manifold but only for 2 dimensional surfaces. Now let us take another surface $N$ (with $V$ as our chart and $τ$ as our function from $R^{2}$ to $N$ ) with the same structure and we have a function $f : M \to N$ then notice that $τ^{- 1} \circ f \circ σ$ is a function from $R^{2} \to R^{2}$ thus we can use regular calculus on it.

Definition

A surface is a Hausdorff topological space which is locally homeomorphic to $R^{2}$ .

Example

Surfaces: $R^{2}$ , any open set in $R^{2}$ , sphere, hyperboloid
Not surfaces: Double Cone (the cone with the vertex removed).

Charts

Definition

If $X$ is a surface, $U$ an open set of $X$ (a patch) and $V$ is a open set of the plane $R^{2}$ . Let:

φ : U \overset{h o m e o m o r p h i s m}{\to} V

is called a chart. A collection of charts ( $φ_{α} : U_{α} \to V_{α}$ ) is called an atlas.

Example

We have the unit sphere (with the north pole removed) as our surface and the stereographic projection is our atlas.
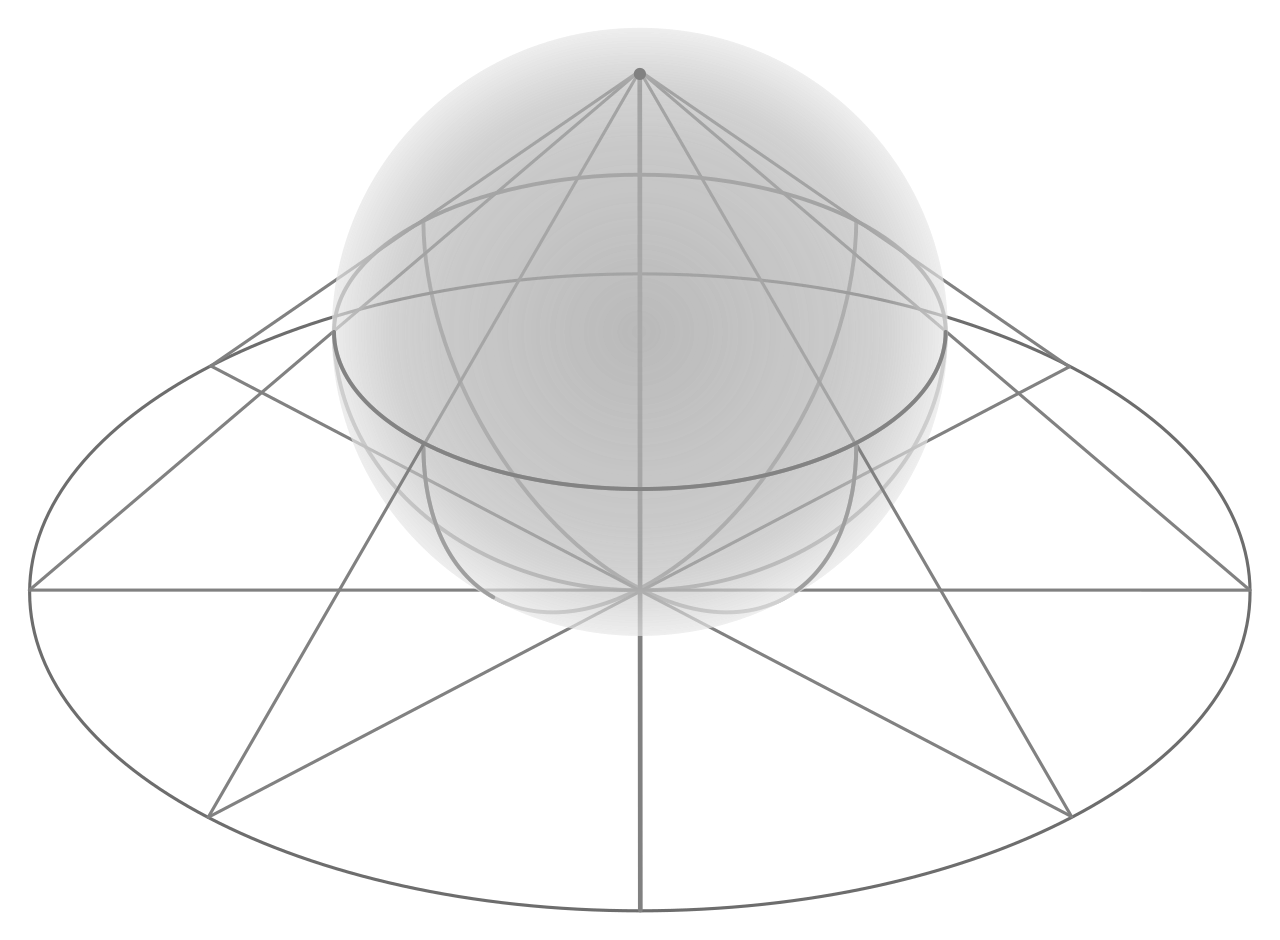
$sphereprojection.png|500$
We take the same unit sphere $S^{2} : {(x, y, z) \in R^{3} : x^{2} + y^{2} + z^{2} = 1}$ then we have the chart:

σ_{1} (θ, ϕ) = (c o s θ c o s ϕ, s i n θ c o s ϕ, s i n ϕ)

It covers MOST of the sphere but we lose information at (some) points to overcome this we can simply add more charts:

σ_{2} (θ, ϕ) = (s i n ϕ, c o s θ c o s ϕ, s i n θ c o s ϕ)

σ_{3} (θ, ϕ) = (s i n θ c o s ϕ, s i n ϕ, c o s θ c o s ϕ)

Orientability

Now let $ϕ : U \to V$ and $ϕ^{'} : U^{'} \to V^{'}$ be two charts with some overlap (that is $U \cap U^{'} \neq \emptyset$ ) then we have a transition map:

ϕ^{'} \circ ϕ : ϕ (U \cap U^{'}) \to ϕ^{'} (U \cap U^{'})

Idea

A surface is orientable if it possesses an atlas from which all the transition maps are orientation preserving.

Mobius strip is not orientable

$Flipping_in_Möbius_strip.gif|500$

Theorem

Any orientable closed surface is homeomorphic to a torus with $g$ holes with $g \geq 0$ .