Session 01 - Introduction to Graph Theory I
A graph
One could represent a graph with a dots to represent the vertices and lines connecting vertices together which represent the edges.
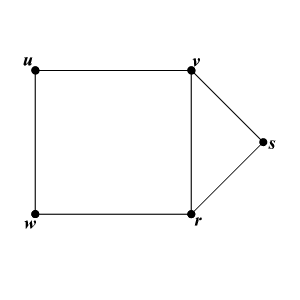
It is possible to have graphs which allows multiple edges to connect the same two vertices,
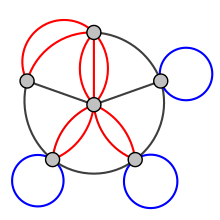
Or even direct the edges.
The set of vertices may be infinite.
A graph with an infinite vertex set or with an infinite edges set is called an infinite graph.
A graph with a finite vertex set and a finite edge set is called a finite graph.
We will usually consider only finite graphs.
A simple graph has undirected graphs, no multiple parallel edges and no loops (edges connecting the same vertex to itself).
Let
If
and are adjacent or neighbors. is incident with and . connects and .
- The set of all neighbours of a vertex
is called the if and is denoted by - The neighbourhood of a set
of vertices is - The degree of a vertex
, denoted by is the number of edges incident with . Each loop contributes twice to the degree of a vertex. - A vertex of degree 0 is isolated.
- A vertex of degree
is pendant.
(The Handshaking Theorem) Let
Each vertex's degree counts an edge twice.
An undirected graph has an even number of vertices of odd degree.
This immediately follows from the handshaking theorem.
An example of an application of the above theorems:
How many graphs are there on
0
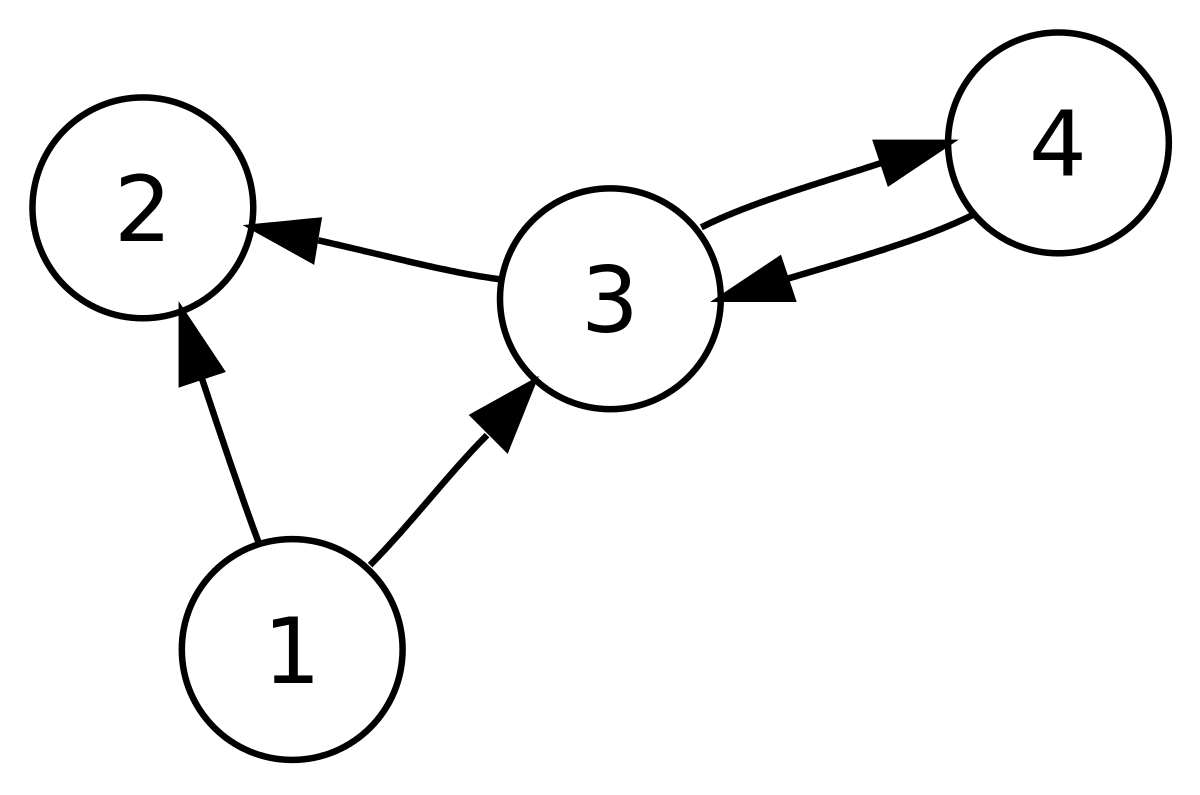
Let
If
is adjacent to and is adjacent from . is the initial vertex and is the terminal vertex of is an out-neighbor of and is an in-neighbour of .
The in-degree of a vertex
The out-degree of a vertex
(The Handshaking Theorem) Let
Some Special Graphs
A complete graph on
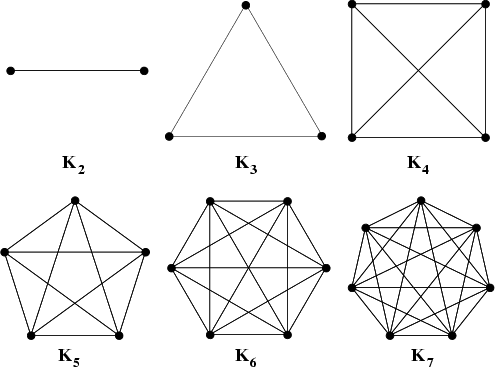
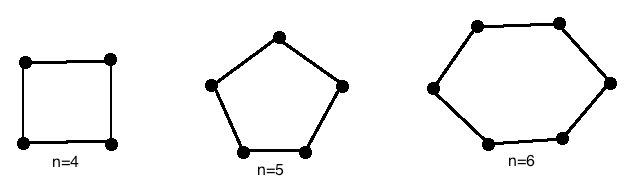
A cycle
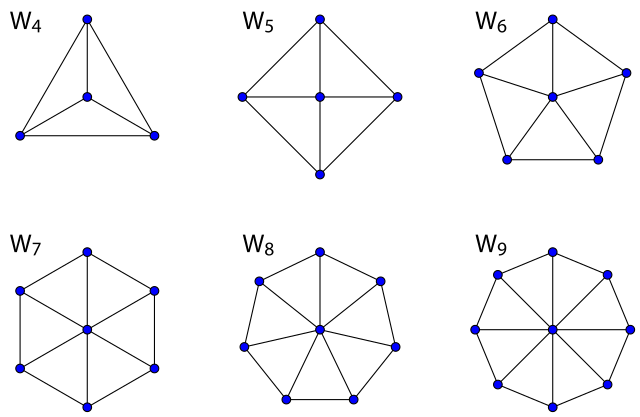
A wheel
An
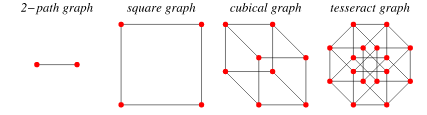
A simple graph
- Every even cycle is a bipartite.
- Every hypercube is bipartite.
is not bipartite
A simple graph is bipartite if and only it is possible to assign two colours to the vertices of the graph in such a way that no two adjacent vertices are assigned the same color.